My original plan was to do several posts about general information and then go deeper into some topics, but as I’m currently working on getting the ST iNEMO LSM9DS1 intertial module to work, I thought that I might as well start this blog on this subject.
One of the thing I would like to achieve with this robot is to get it as close as possible of being capable of navigating and avoiding obstacles autonomously so it can, for example, returns to its starting position by itself.
As it will be used mostly indoor, using a GPS for precise positioning is not possible, so we have to rely on less accurate sensors. A 9DOF inertial module in the form of a LSM9DS1 from ST(datasheet), will be the main sensors to evaluate the robot position. This chip is in reality two components into a single package with a 3D accelerometer / gyroscope on one side, and a 3D magnetometer (compass) on the other side.
This kind of sensors are cheap, and are able to give the acceleration, the angular speed, as well as measuring the magnetic field but they are also not very accurate. For instance, apart from the usual “noise” of the measurement, gyroscope has an output drift which is dependant of the chip temperature and the magnetometer is subject to several measurement impairment due to the presence of other magnetic components (especially in a robot were motors are close !!!). It is possible to mitigate some of the errors by performing a sensor calibration without completely removing them. Also if we want to be able to evaluate the speed and position of the robot based on the accelerometer, we need to remove the acceleration due to the gravity which means we need to be able to evaluate precisly the direction of the gravity in the sensor reference frame.
That’s where the filter proposed by Sebastian Madgwick comes into play (more info). This filter combines data from the gyroscope, accelerometer and magnetometer to estimate the orientation (in the form a quaternion) of the device according to the earth reference (magnetic north and gravity). This algorithm acheive a good accuracy even if the device is subject to linear accelerations and is robust to sensors bias and drift. It is also open source and C code is available!
So, everything perfect, right? Not really and I have been struggling a little bit to get the correct output from the filter. Main reason for that the source code of the filter does not provide any documentation about the convention used for the input values: unit and axis orientation. So I had to dig into Sebastian Madgwick’s paper to find some info.
Units are simples. The filter needs to have the gyroscope data expressed as rad.s-1. For the acceleration and magnetic field, however, you can use any unit you like, because the values are normalized in the filter (only the vector orientation is important).
However, getting a clear answer about the axis orientation was difficult. On some discussion I found that the madgwick filter’s is using a NED (x pointing north, y pointing east and z pointing down) convention just like in aviation. This is not completely correct. Madgwick’s filter is indeed using a right handed axis convention but as show in Madgwick paper on page 5, the Z axis is pointing up and not down.
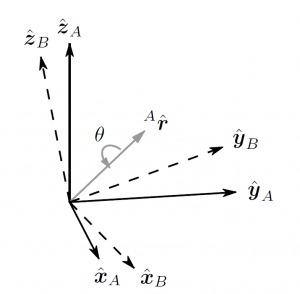
This can also be confirmed by the Xsens MTX user Manual which was used to perform the algorithm evaluation and is using the same convention.
Where it gets a little bit confusing, is that Madgwick is giving the formulae to get the euler angles from the quaternion representation in his paper.
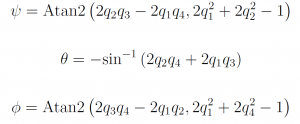
Where ψ is yaw, θ is pitch and Φ is roll.
If you use theses equations, the calculated roll, pitch and yaw will be according to the aircraft convention (NED), but for the roll which need to be inverted.
Finally, Madgwick is using variables q0, q1, q2 and q3 (or q1, q2, q3 and q4 in his paper) to represent the quaternion. But sometimes you can find quaternion represented as x, y, z and w (as in unity 3D). If for some reason, you want to use the filter output for something else, just be aware that w is equivalent to q0, not q3.
So now that we know what is expected by the filter, what about the output of the LSM9DS1 ? For accelerometer/gyroscope, the datasheet is giving the following:
Orientation reference is left handed, so we can’t use the output as it is but swapping from left handed to right handed axis is easy, we just have to swap the X and Y axis for gyro and accelerometer. Finally we have to align the X axis point to the front of the robot (and Y to be the left side). For Yapibot, I got lucky as the Y axis of the sensor is pointing to the front of the robot so I can just apply:
Yapibot.ax = LSM9DS1.ay
Yapibot.ay = LSM9DS1.ax
Yapibot.az = LSM9DS1.az
And for the gyro:
Yapibot.gx = LSM9DS1.gy
Yapibot.gy = LSM9DS1.gx
Yapibot.gz = LSM9DS1.gz
The same way, we need to adapt the ouput of the magnetometer according to our reference.

Be careful here because for some reason, ST did not use the same orientation of the diagram (dot on the chip is up, while for accel/gyro it is on the left) (IT’S A TRAP!). So finally, compared to the accel/gyro, only the X direction is inverted.
Yapibot.mx = LSM9DS1.my
Yapibot.my = -LSM9DS1.mx
Yapibot.mz = LSM9DS1.mz
Using this convention, I have been able to correctly get the orientation of the robot.


Hi lythaniel,
We are trying to implement Madgwick’s algorithm to find orientation. Your blog was very useful and gave us a new direction of thinking and even helped us correct the misalignment of axis of gyro chip with respect to accelerometer in Adafruits 10 dof board.
After the above correction, we are getting accurate results for roll and pitch. However, yaw is 20° inclined, pointing downwards, towards the ground with respect to horizontal plane (ref X axis), which we actually found out to be equal to the magnetic inclination or dip at our location. This results in displaying 20° when facing north, 90°/270° facing east or west, similarly affecting the south. We are not able to correct this and bit confused in this regard, as the Madgwick’s algorithm is taking the reference for True North at 20° inclined position.
Did you face similar issue? and if yes how did u correct the same
Hi Krupal,
No, I don’t have such issue and I don’t recall having such problems. Magnetic sensors raw value often show non “linear” output due to local magnetic sources (like motors) or magnetic north inclination but I would expect the AHR to cope with that. Did you try to play with the beta parameter ? A low value can cause the algorithm to takes time to converge to a good estimation, high value will make it instable.
Also for my project, I implemented a calibration of the sensors to improve the accuracy, it may helps in your case. Have a look here for more details. Code is also available on github.
Hi lythaniel,
Thanks for your reply. I haven’t played with beta yet, as currently I have set it to 1 and getting good results, but will now try with different values for beta and check its effect.
I have already calibrated the sensors (accelerometer and magnetometer) using Magneto tool. I will use your calibration code and check if that helps. Thanks for your suggestions.
Hi lythaniel,
Thank you for your awesome tutorial!
I have some problems with the LSM9DS1 and I hope you could help me out. I followed your implementation of the madgwick filter and tried to get the euler angles from the quaternion. But somehow they are completely wrong.
The angles themselves are not just wrong from a stationary point (eg. north isn’t north and pitch and roll aren’t even near 0 on a flat surface) but they also change wrong. When I rotate my sensor 90° the corresponding angle changes around 20°.
I tried changing beta, the frequency and checked if the math behind the quaternions is correct but still I get wrong angles. Can you please help me out??
Hi Robert,
There is not much you can do on the filter side anyway so my guess is more that your sensor output is incorrect. Especially the output of the magnetometer as it may be affected by local magnetic field like motors and such. If that’s the case, then running a calibration should solve the issue.